米国株は上がりすぎじゃない?
SP500はまだ上がる??
チャートを見ると、右肩上がりを続けていてバブルのようにも見えますよね。
良い加減もう上がり過ぎで、頭打ちになるのでは?と心配される声も聞くことがあります。
 Y-bow
Y-bow今後は上がらないということであれば、これから投資を始める方やこれから生まれてくる子供が不憫でなりません。。。
結論、今後も上がっていくので全く心配は不要でしょう。


NASDAQを例に挙げて説明した記事で説明していますので、株価が上がり続ける根拠は以下の記事を参照して下さい。


この記事ではNASDAQ100よりも多くの銘柄に分散投資が可能な人気インデックス、S&P500に着目して『バブル的な上昇をしているのか?』を解説します。
特に “いつの時代も” 直近の株価がバブルに見える現象についてはより詳細に、実際のチャートを用いて説明します。
これを読めば、今の株価が高すぎるということは無く、また今後も上がっていくであろうことを納得出来ると思います。


- 投資家・個人事業主・医学博士
- 投資歴15年 (学生時代から)
- レバナス/USA360/3倍ETFをメインに積立中
- 地銀→野村證券→ネット証券
- FIRE済み:好きで働いてます
いつでもバブルの様相を見せるS&P500
先ずは実際のチャートを見てみましょう。
S&P500の1956年以降のチャート(2022年2月末時点)は以下の通りです。
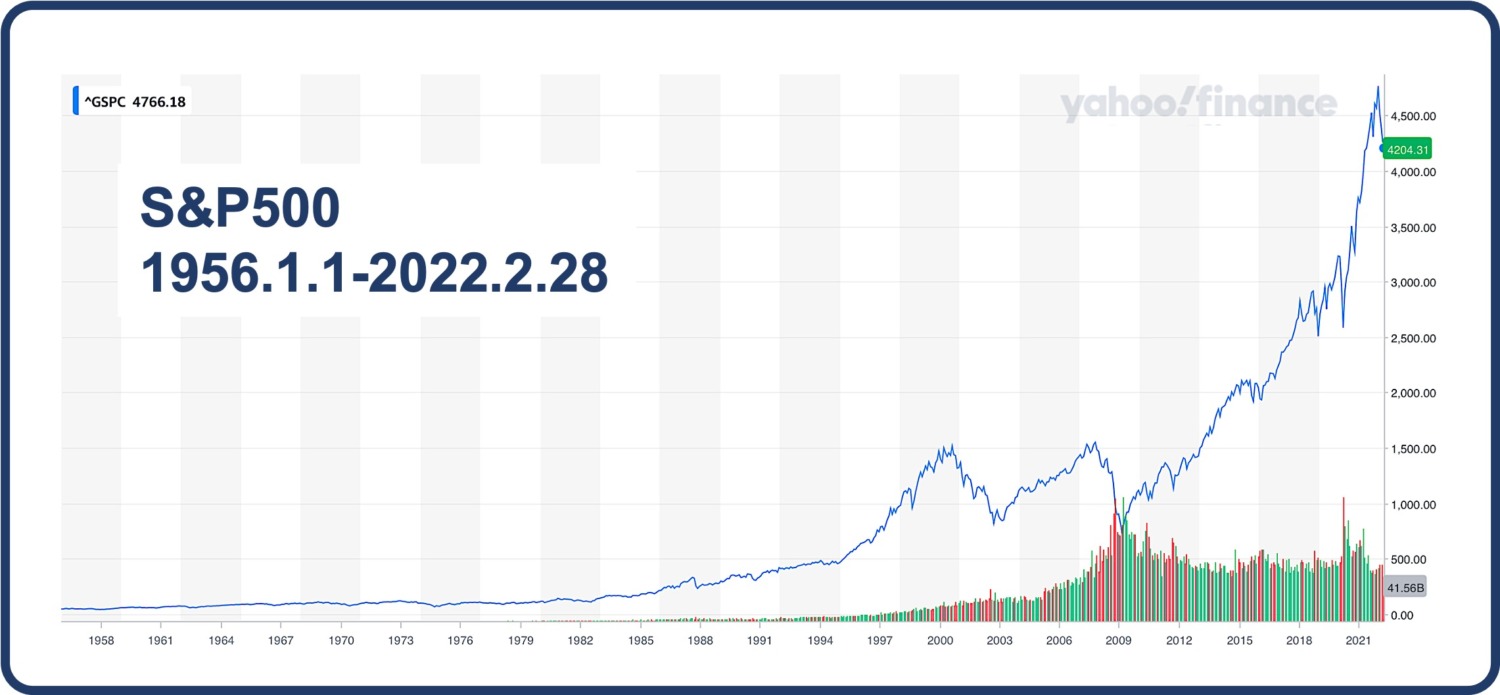

確かに急激な高騰が見て取れます、最高で4766まで上昇しています。
いかにもバブルかのような、近年の上昇ぶりが目立ちます。



しかし本当にそうでしょうか?
少しずつ過去の時点にずらして行ってみましょう。
2019年12月末時点に遡ると、チャートは以下の通りでした。
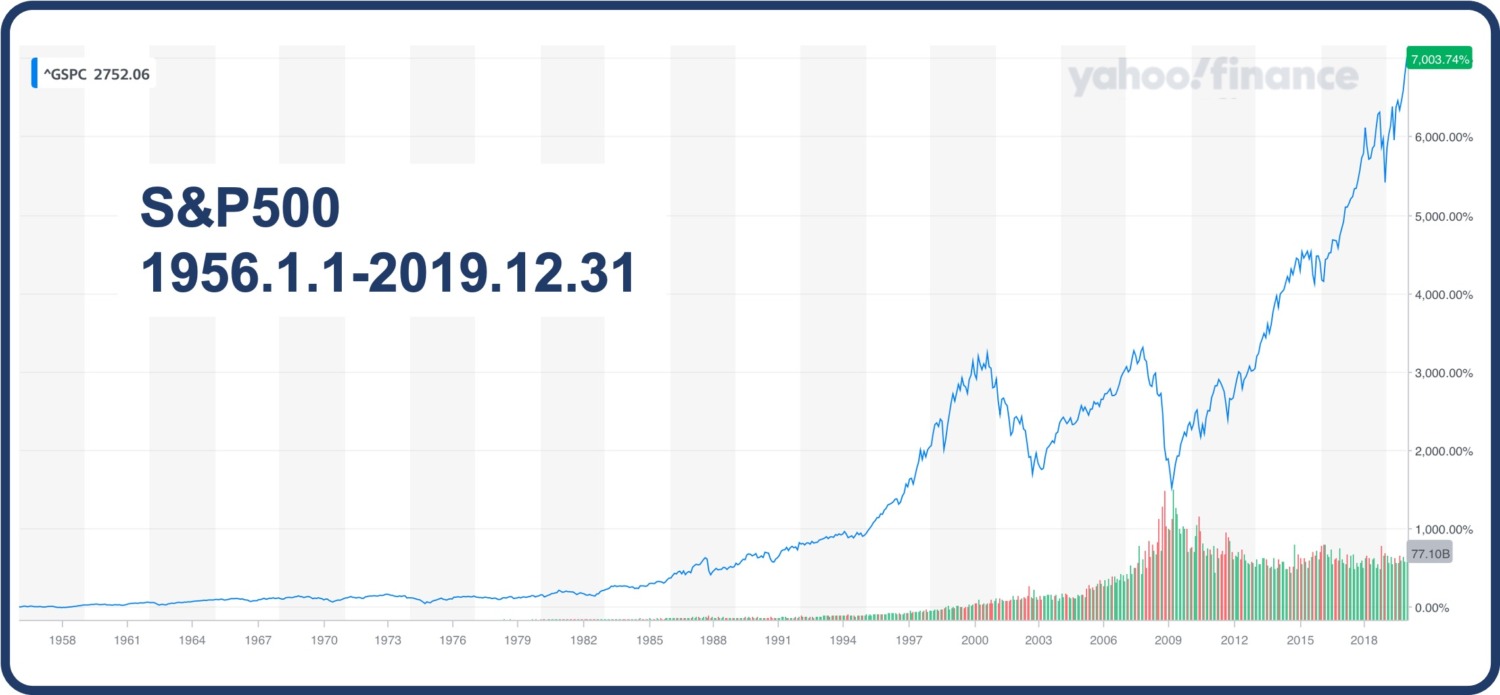

バブルの様相ですね、この時点も中々の急騰ぶりです。
2752まで上昇しています(1956年時点と比較すると7,000%超え)。
さらに遡り、1999年12月末時点です。
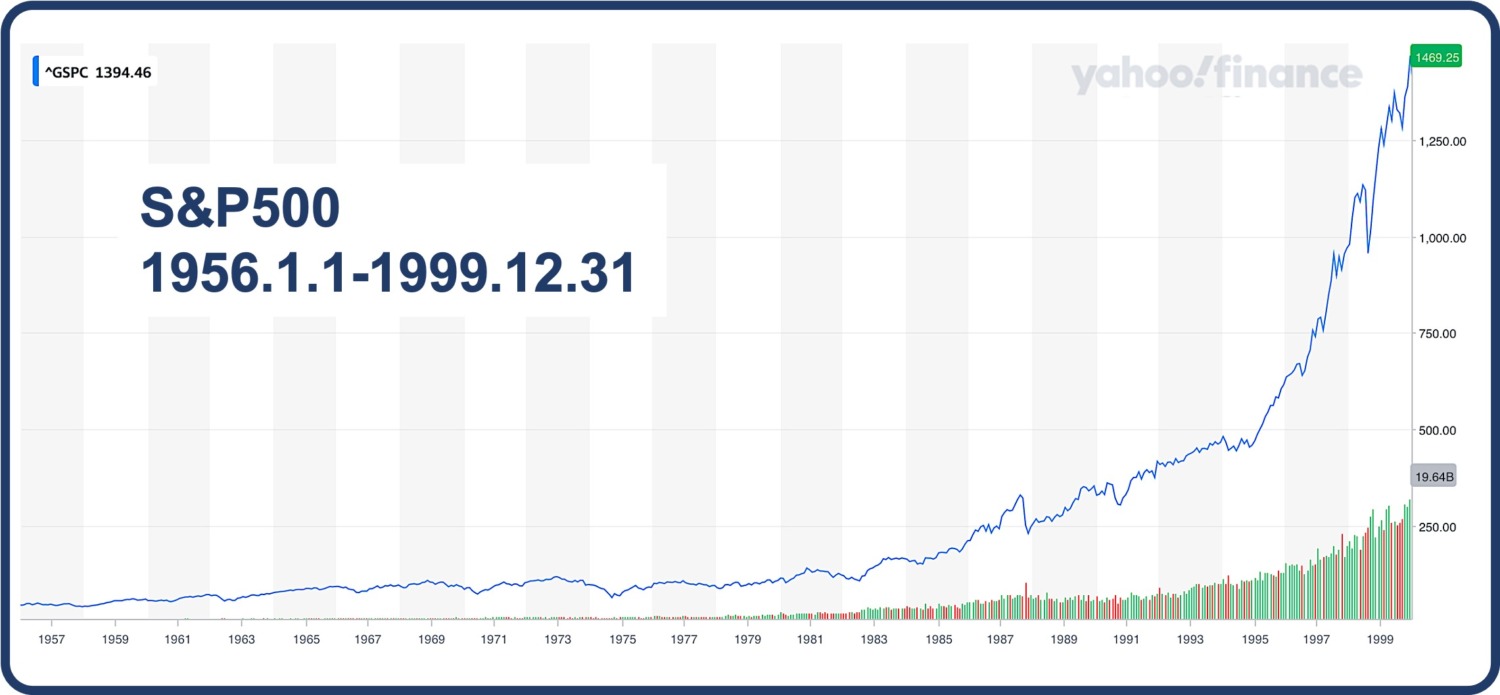

相変わらずすごいバブルの様相ですね。
1469まで上がっています。
さらにさらに遡ってみましょう。
以下のチャートは1987年8月末までのチャートです。
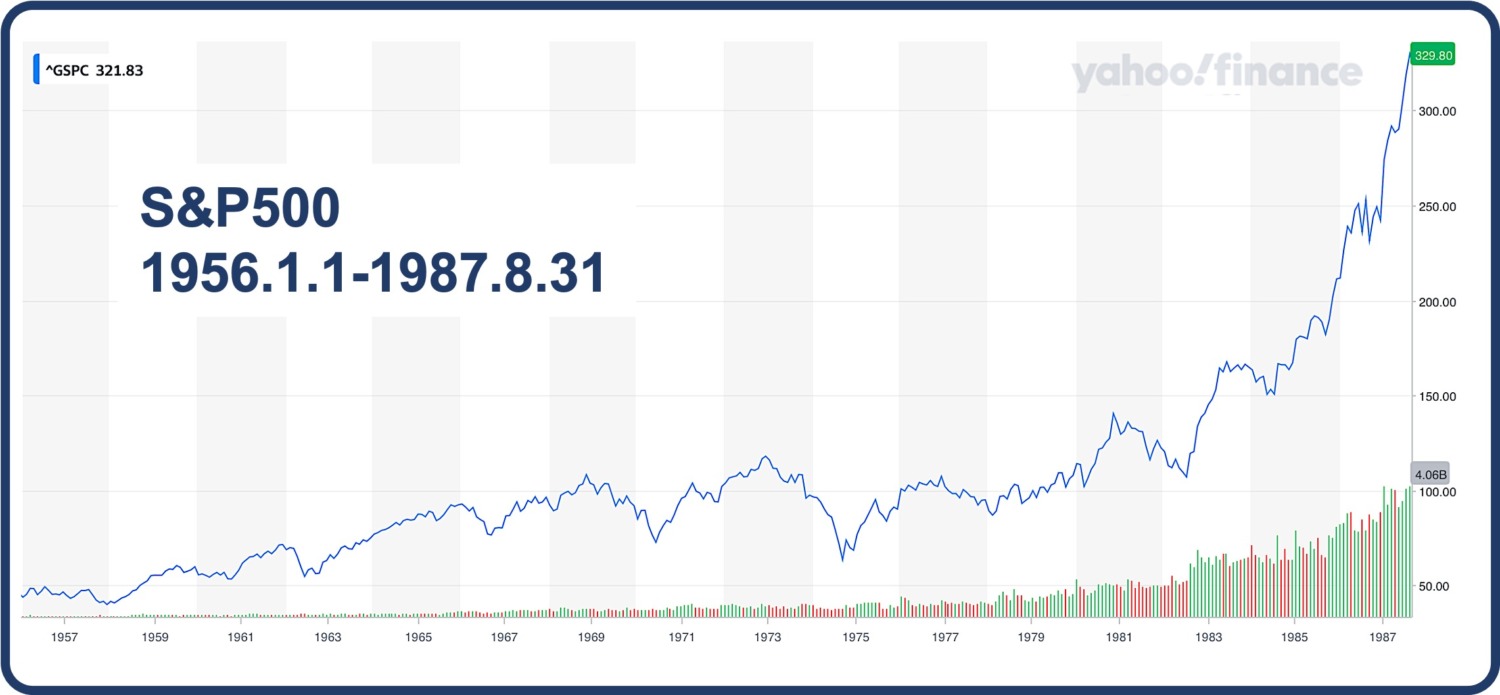

相変わらずバブルの様相ですね。。。
329まで上がっています。
ということは、ここまで見ただけでももう35年間(1987-2022)もバブルが続いていることになります。



もう何が言いたいのか分かりますよね。
皆さんが普段目にしているLinear表示(%表示でも同様)では、一定のペースで(例えば毎年4%ずつ)上昇していくチャートを見るとどの時点でもバブルのように見えます。
当然です。
100の4%は4ですが、1,000の4%は40です。
同じ4%の上昇でも4上がるのと40上がるのとでは見た目が大きく異なります。
それは縦軸が割合変化に適した表示方法になっていないためですので仕方がありません。
では、どうすれば適した表示にすることが出来るでしょうか。
対数チャートで見るS&P500
バブルに見えるLinear表示のチャートも、縦軸をLog表示(対数表示)にすることで上昇ペースを正しく把握することが出来るようになります。
最初に紹介したS&P500の1956年からのチャートで実際に見てみると、以下の通りです。
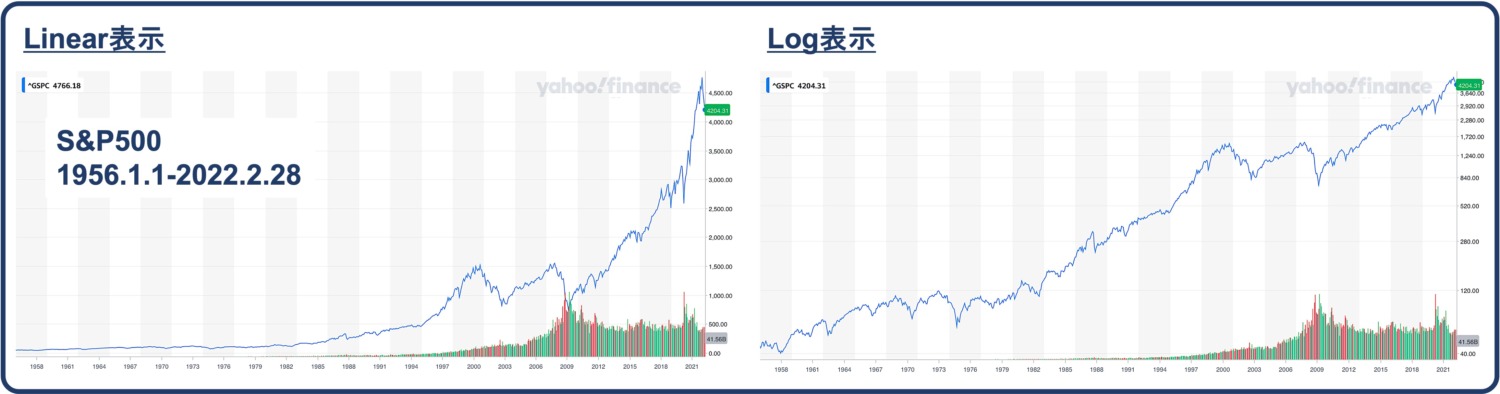

左側に示した『バブルに見える』チャートも、対数表示にすると直線的に右肩上がりになっているのが分かります。
先ほどのように時期を遡って確認してみましょう。
2019年12月末までのチャートをLinear表示とLog表示で比較したものは以下の通りです。
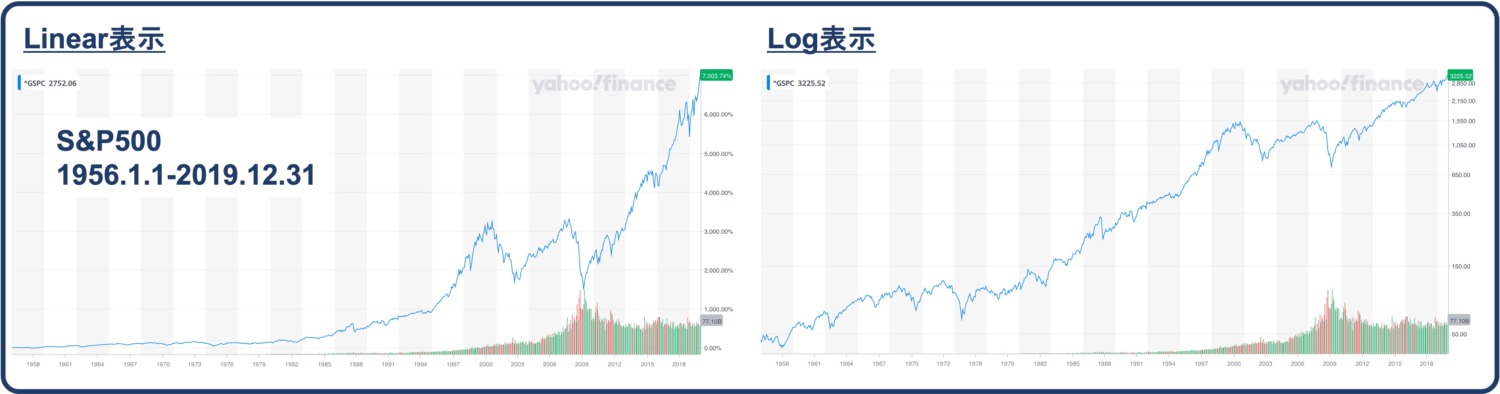

印象は2021年までと変わらないですね。
お気付きかもしれませんが、Log表示はLinear表示と違ってどの期間を切り取ってみてもグラフの形が全く変わりません。
もともと増減の割合が反映されていますので、切り取った部分がただ同じ形のまま表示されています。
折角なので1987年8月末までのチャートも示してみます。
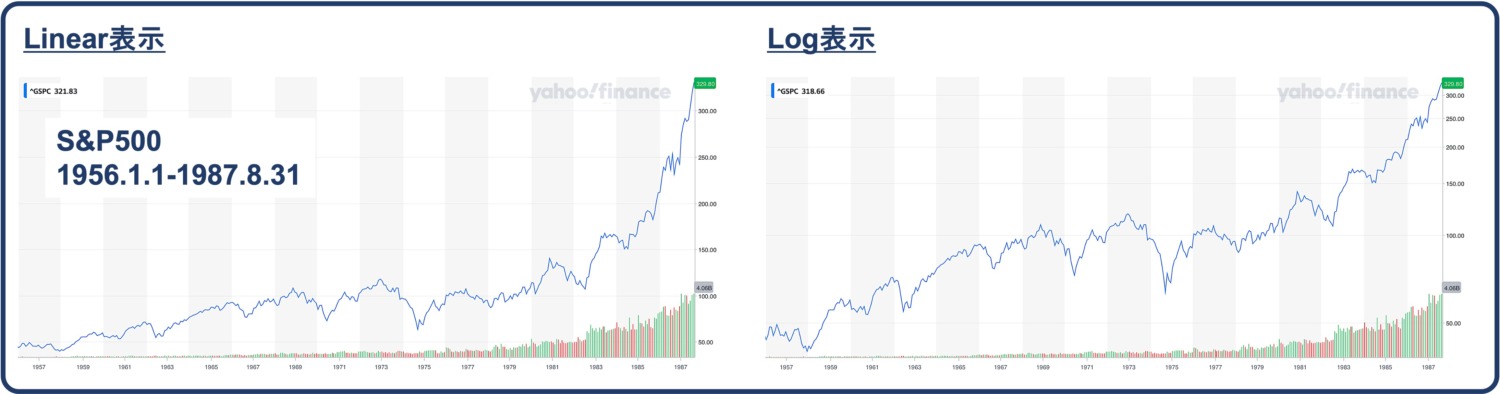

相変わらず対数表示では直線的な上昇です。
この対数チャートは2022年までのチャートに表示されている1987年までの部分と全く同じ形です。
一方でLinear表示は切り取る期間によって全く印象が変わってしまうのです。
それがよく分かるように、切り取った期間がどのように『見えるのか』を以下に比較してみました。
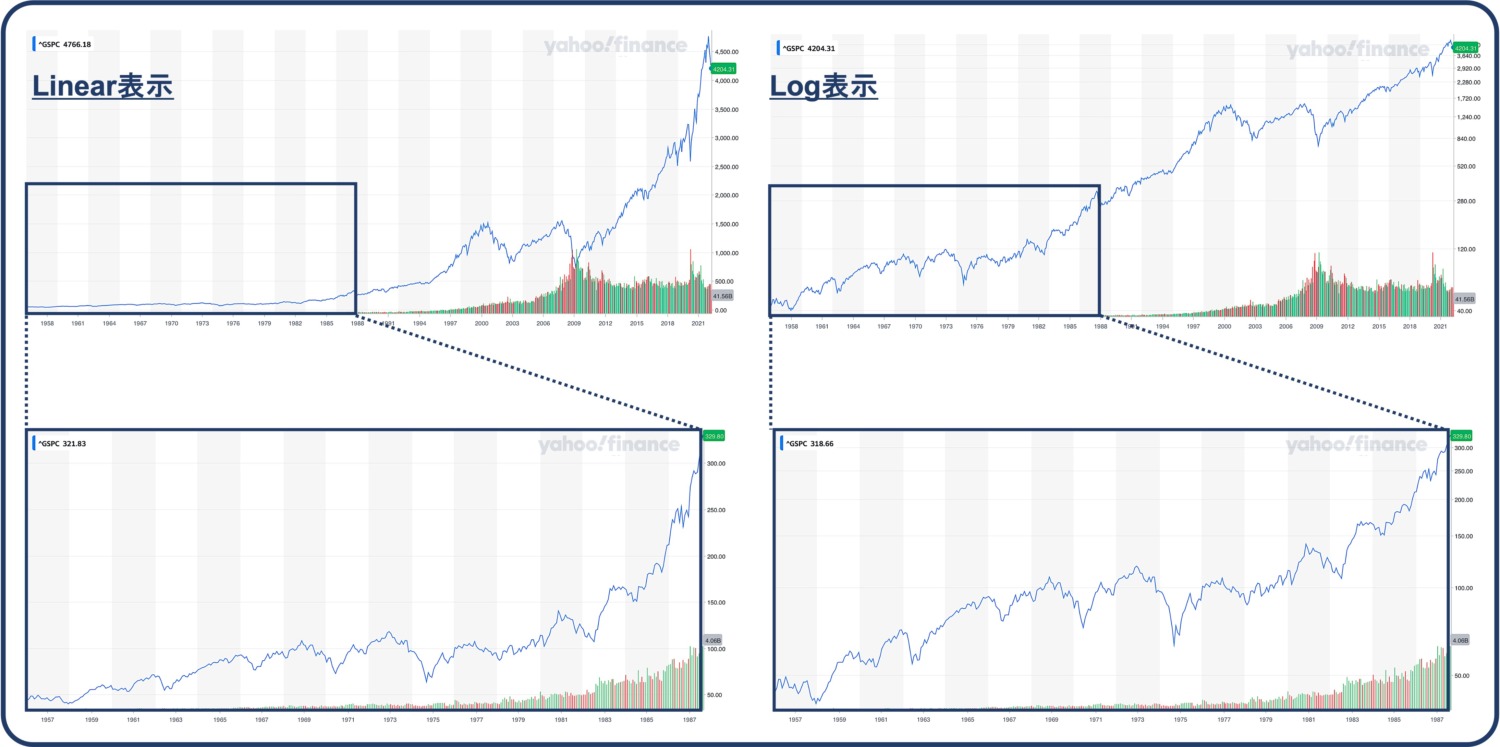

Linear表示では、2022年までの期間を表示していた時には1987年まではとてもなだらかで、バブルの様相は全く感じませんでした(左上)。
ところが、1987年までを切り取って見てみると、途端に1983年以降は急騰してバブルかのように映ります(左下)。
一方Log表示であれば、2022年までの表示であっても1987年までの表示であっても、1987年までの期間のチャートの形は全く同じで、虫眼鏡で拡大しただけのように見えます。
今後も上昇を続けると考える根拠
S&P500が上がり過ぎということは無く、むしろ健全に一定割合での成長を続けてきていることは分かりました。
ではこの先も同じように上がり続けると考えても良いのでしょうか。
未来のことは(少なくとも2022年現在の科学水準では)誰にも確定的なことは分かりません。
参考になるのは過去の動向と伸び代の可能性だけです。
過去の動向については、数々の暴落や戦争を経験してきた人類史での超長期株価推移を見れば分かります。
以下の記事に詳細を説明していますが、現金や債券を含めても株式だけがずっと右肩上がりを続けてきた唯一のアセットであることが明らかです。


だから今後も上がる、ということでは確かにありませんが、人類は常に新しい価値を生み出しており、今この瞬間に働いている方が、そして休み無く働いているコンピューター(A.I.)が、それを継続しているのです。
日本はすでに人口減少が始まっていますが、世界の人口はまだ増加を続けています。
そして先進国の中でも技術開発の素地(投資環境)が出来上がっている米国だけは人口が減らず、今後も当面は地球の価値向上の中心地であり続けることでしょう。
その中心地が米国で無くなれば、その時に地球の中心を担う国家や集団がその価値を高め続けることでしょう。
地球文明はまだまだ伸び代が大きく、その伸び代は我々の想像を遥かに超えるものです。



私自身が科学者なので身に染みて分かりますが、人類が目指している研究成果は果てしなく広がっています。
今はまだ夢物語かもしれませんが、一昔前までは病院の検査機器や携帯電話も夢物語で、飛行機で空を飛ぶことさえ当たり前ではなかったのです。
そしてこの先には、以下のように圧倒的な技術革新も待っていることでしょう。


そしてそれらを成し遂げるまで、S&P500或いは全世界株は上がり続けることでしょう。
50年後、100年後にこの記事がもし残っているようなことがあれば、その時代の方々に是非コメントして頂きたいものです。
2022年当時の株価はバブルだったでしょうか?
終わりに:S&P500の値動き
S&P500はNASDAQ100よりも分散が効いていることもあり、値動きが比較的穏やかな傾向にあります。
それでも長期的に見るとご覧頂いた通りかなりの値上がりを記録しており、ともすればバブルかと思われる場合もあるようです。
しかし一定の割合で成長し続ける時のチャートの理解は説明した通りで、適宜対数チャートで確認するようにしましょう。
例えば国の成長を知るためのGDP成長率というものを目にすることがあると思います。
GDPの成長も『割合=率』で表します。
当然、成長した社会がさらに成長する時には、小さな社会が成長する時よりも絶対値では大きく成長するからです。
ドングリを拾い、イノシシを狩っていた頃と同じ単位で進歩を表していたら、正確に把握出来なくなってしいますよね。



この10年で増えたGDPはドングリ何個分でしょうか。。。
投資は長期的に行うこと、とはよく言われますが、長期的な視点をしっかり持っておくことは不安を払拭することに繋がります。









コメント